Lời giải của Tự Học 365
Giải chi tiết:
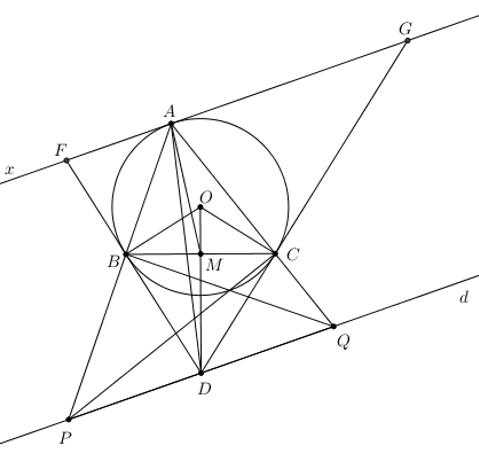
1) Chứng minh tứ giác OBDC nội tiếp đường tròn.
Do DB, DC là các tiếp tuyến của đường tròn (O) (Rightarrow widehat{OBD}=widehat{OCD}={{90}^{0}})
Xét tứ giác OBDC có (widehat{OBD}+widehat{OCD}={{90}^{0}}+{{90}^{0}}={{180}^{0}}Rightarrow ) tứ giác OBDC là tứ giác nội tiếp (Tứ giác có tổng hai góc đối bằng 1800)
2) Gọi M là giao điểm của BC và OD. Biết (OD=5cm). Tính diện tích của tam giác BCD.
Áp dụng định lí Pitago trong tam giác vuông OBD có (BD=sqrt{O{{D}^{2}}-O{{B}^{2}}}=sqrt{{{5}^{2}}-{{3}^{2}}}=4,,left( cm right))
Ta có (OB=OC=R;,,DB=DC) (tính chất hai tiếp tuyến cắt nhau)
(Rightarrow O;,,D) thuộc trung trực của BC (Rightarrow OD) là trung trực của BC (Rightarrow ODbot BC).
Áp dụng hệ thức lượng trong tam giác vuông OBD có:
(DM.DO=D{{B}^{2}}Rightarrow DM=frac{D{{B}^{2}}}{DO}=frac{{{4}^{2}}}{5}=frac{16}{5},,left( cm right))
(BM.OD=OB.BDRightarrow BM=frac{OB.BD}{OD}=frac{3.4}{5}=frac{12}{5},,left( cm right))
Vậy ({{S}_{Delta DBC}}=frac{1}{2}DM.BC=DM.BM=frac{16}{5}.frac{12}{5}=frac{192}{25}=7,68,,left( c{{m}^{2}} right)).
3) Kẻ đường thẳng d đi qua D và song song với đường tiếp tuyến với (O) tại A, d cắt các đường thẳng AB, AC lần lượt tại P, Q. Chứng minh (AB.AP=AQ.AC)
Ta có (widehat{APQ}=widehat{xAB}) ( 2 góc so le trong do đường thẳng Ax // PQ)
Mà (widehat{xAB}=widehat{ACB}) (góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung cùng chắn cung AB của (O)).
(Rightarrow widehat{APQ}=widehat{ACB})
Xét tam giác ABC và tam giác AQP có:
(widehat{PAQ}) chung;
(widehat{APQ}=widehat{ACB},,left( ,cmt right))
(Rightarrow Delta ABCbacksim Delta AQP,,left( g.g right)Rightarrow frac{AB}{AQ}=frac{AC}{AP}Rightarrow AB.AP=AC.AQ)
4) Chứng minh góc PAD bằng góc MAC.
Kéo dài BD cắt D tại F.
Ta có (widehat{DBP}=widehat{ABF}) (đối đỉnh)
Mà (widehat{ABF}=widehat{ACB}) (góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây cung cùng chắn cung AB)
(widehat{ACB}=widehat{APD}) (do (Delta ABCbacksim Delta AQP))
(Rightarrow widehat{DBP}=widehat{APD}=widehat{BPD}Rightarrow Delta DBP) cân tại D (Rightarrow DB=DP)
Tương tự kéo dài DC cắt d tại G, ta chứng minh được (widehat{DCQ}=widehat{ACG}=widehat{ABC}=widehat{DQC}Rightarrow Delta DCQ) cân tại D (Rightarrow DC=DQ)
Lại có (DB=DC) (tính chất hai tiếp tuyến cắt nhau) (Rightarrow DP=DQRightarrow D) là trung điểm của PQ.
Ta có: (Delta ABCbacksim Delta AQP,,left( cmt right)Rightarrow frac{AB}{AQ}=frac{AC}{AP}=frac{BC}{PQ}=frac{2MC}{2PD}Rightarrow frac{AC}{AP}=frac{MC}{PD})
Xét tam giác (AMC) và tam giác (ADP) có
(widehat{ACM}=widehat{APD},,left( widehat{ACB}=widehat{APQ},,left( cmt right) right))
(frac{AC}{AP}=frac{MC}{PD},,left( cmt right))
(Rightarrow Delta AMCbacksim Delta ADP,,left( c.g.c right)Rightarrow widehat{PAD}=widehat{MAC},,left( dpcm right)).
Chọn B


