Toán 7 (Chân trời sáng tạo): Bài tập cuối chương 1

Giải bài tập Toán 7 Bài tập cuối chương 1

Video giải bài tập Toán 7 Bài tập cuối chương 1

Bài tập

Giải Toán 7 trang 27Tập 1

Bài 1 trang 27 Toán lớp 7 Tập 1: Thực hiện phép tính:

a) 25+35:−32+12;

b) 213+−132−32;

c) 78−0,25:56−0,752;

d) −0,75−−2+32:1,5+−54

Lời giải:

a) 25+35:−32+12=25+35.−23+12

=25+−25+12=25+−25+12=12.

b) 213+−132−32

=73+19−32

=4218+218−2718

=1718.

c) 78−0,25:56−0,752

=78−14:56−342

=78−28:1012−9122

=58:1122=58:12122

=58.122=5.1448=90.

d) −0,75−−2+32:1,5+−54=−34−−42+32:32+−54

=−34+−54−−12.23=−2−−13=−2+13=−63+13=−53.

Bài 2 trang 27 Toán lớp 7 Tập 1: Thực hiện phép tính (bằng cách hợp lí nếu có thể)

a) 523+717+0,25−523+1017;

b) 37.223−37.112;

c) 1314:−47−1714:−47;

d) 100123:34+712+23123:95−715.

Lời giải:

a) 523+717+0,25−523+1017

=523−523+717+1017+14

=0+1+14=44+14=54.

b) 37.223−37.112

=37.83−37.32=3783−32

=37166−96=37.76=12.

c) 1314:−47−1714:−47

=13+14.−74−17+14−74

=−74.13+14−17−14

=−74.13−17+14−14

=−74.−4=7.

d) 100123:34+712+23123:95−715

=100123:912+712+23123:2715−715

=100123:1612+23123:2015

=100123:43+23123:43

=100123.34+23123.34

=34.100123+23123

=34.123123=34.

Bài 3 trang 27 Toán lớp 7 Tập 1:

a) 516.2771255.911;

b) −0,22.5−213.27346.95;

c) 56+22.253+23.125226.56.

Lời giải:

a) 516.2771255.911=516.337535.3211

=516.33.753.5.32.11=516.321515.322=53.

b) −0,22.5−213.27346.95

=−152.5−213.333226.325

=152.5−213.39212.310

=15.5.5−212.2.39212.39.3

=15−23

=315−1015

=−715.

c) 56+22.253+23.125226.56

=56+22.523+23.53226.56

=56+22.52.3+23.53.226.56

=56+22.56+23.5626.56

=561+22+2326.56=56.1326.56=12.

Bài 4 trang 27 Toán lớp 7 Tập 1: Tính giá trị các biểu thức sau:

a) A=−0,5−35:−3+13−−16:−2;

b) B=225−0,036:1150−314−249.929.

Lời giải:

a) A=−0,5−35:−3+13−−16:−2

=−12−35.−13+13−−16.−12

=−510−610.−13+13−−1.−16.2

=−1110.−13+13−112

=1130+13−112

=2260+2060−560

=3760

Vậy A=3760.

b) B=225−0,036:1150−314−249.929

=225−361  000.5011−3+14−2+49.929

=225−9250.5011−3+14−2−49.929

=20250−9250.5011−1+14−49.929

=11250.5011−3636+936−1636.929

=15−2936.929=15−14

=420−520=−120.

Vậy B=−120.

Bài 5 trang 27 Toán lớp 7 Tập 1: Tìm x, biết:

a) −35x=1225;

b) 35x−34=−112;

c) 25+35:x=0,5;

d) 34−x−12=123;

e) 2215:13−5x=−225;

g) x2+19=53:3.

Lời giải:

a) −35x=1225

x=1225:−35

x=1225.−53

x=−45

Vậy x=−45

b) 35x−34=−112

35x−34=−32

35x=−32+34

35x=−64+34

35x=−34

x=−34:35

x=−34.53

x=−54

Vậy x=−54

c) 25+35:x=0,5

25+35:x=12

35:x=12−25

35:x=510−410

35:x=110

x=35:110

x=35.10

x=6

Vậy x=6

d) 34−x−12=123

34−x−12=53

x−12=34−53

x=912−2012+12

x=−1112+612

x=−512

Vậy x=−512

e) 2215:13−5x=−225

3215:13−5x=−125

13−5x=3215:−125

13−5x=3215.5−12

13−5x=4.8−5.−3.−54.3

13−5x=−89

5x=13−−89

5x=39+89

5x=119

x=119:5

x=119.15

x=1145

Vậy x=1145

g) x2+19=53:3

x2=53.13−19

x2=59−19

x2=49

Trường hợp 1. x2=232

x=23

Trường hợp 2. x2=−232

x=−23

Vậy x = 23; x = −23.

Bài 6 trang 27 Toán lớp 7 Tập 1:

a) Tính diện tích hình thang ABCD có các kích thước như hình sau:

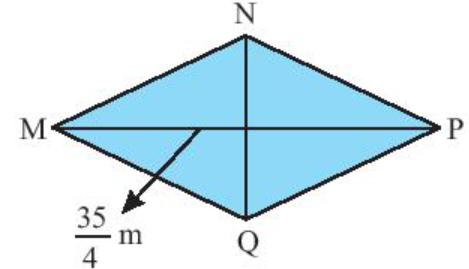
b) Hình thoi MNPQ có diện tích bằng diện tích hình thang ABCD ở câu a, đường chéo MP = 354 m. Tính độ dài NQ.

Lời giải:

a) Diện tích hình thang ABCD bằng:

113+172.32=32.226+516=32.736=734 (m2).

b) Do diện tích hình thoi MNPQ bằng diện tích hình thang ABCD ở câu a nên diện tích hình thoi MNPQ bằng 734m2.

Ta có diện tích MNPQ bằng MP.NQ2 nên độ dài NQ bằng:

2.734:354=732.435=14635 (m).

Vậy độ dài NQ bằng 14635 m.

Giải Toán 7 trang 28Tập 1

Bài 7 trang 28 Toán lớp 7 Tập 1: Tìm số hữu tỉ a, biết rằng lấy a nhân với 12 rồi cộng với 34, sau đó chia kết quả cho −14 thì được số −334.

Lời giải:

Do a nhân với 12 rồi cộng với 34, sau đó chia kết quả cho −14 thì được số −334 nên ta có: a.12+34:−14=−334

a.12+34:−14=−154

a.12+34=−154.−14

a.12=1516−34

a.12=1516−1216

a.12=316

a=316:12

a=316.2

a=38

Vậy a=38

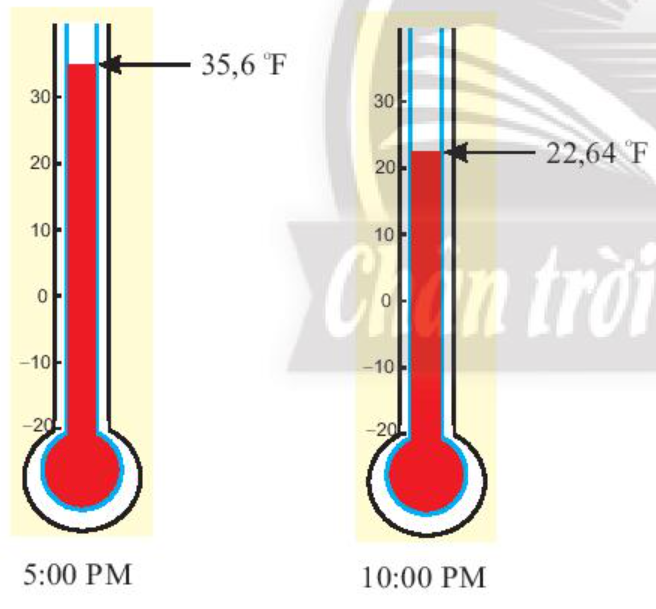
Bài 8 trang 28 Toán lớp 7 Tập 1: Nhiệt độ ngoài trời đo được vào một ngày mùa đông tại New York (Mĩ) lúc 5 giờ chiều là 35,6 oF, lúc 10 giờ tối cùng ngày là 22,64 oF (theo: https:// www.accuweather.com)

Biết công thức chuyển đổi từ độ F sang độ C là:

ToC=59.ToF−32

a) Hãy chuyển đổi các số đo nhiệt độ theo độ F nêu ở trên sang độ C.

b) Tính độ chênh lệch nhiệt độ từ 5 giờ chiều đến 10 giời tối (theo đơn vị độ C).

Lời giải:

a) Nhiệt độ lúc 5 giờ chiều tại New York theo độ C là:

5935,6−32=59.3,6=5.0,4=2 (°C).

Nhiệt độ lúc 10 giờ tối tại New York theo độ C là:

5922,64−32=59.−9,36=5.−1,04=−5,2 (°C).

Vậy nhiệt độ lúc 5 giờ chiều tại New York là 2 oC, nhiệt độ lúc 10 giờ tối tại New York là -5,2 °C.

b) Độ chênh lệch nhiệt độ từ 5 giờ chiều đến 10 giờ tối tại New York theo đơn vị độ C là: 2 - (-5,2) = 2 + 5,2 = 7,2 oC.

Vậy độ chênh lệch nhiệt độ từ 5 giờ chiều đến 10 giờ tối tại New York là 7,2 oC.

Bài 9 trang 28 Toán lớp 7 Tập 1: Mẹ bạn Minh gửi tiết kiệm 300 000 000 đồng vào một ngân hàng theo thể thức kỳ hạn 1 năm. Hết thời hạn 1 năm, mẹ bạn Minh nhận được cả vối lẫn lãi là 321 600 000 đồng. Tính lãi suất ngân hàng theo thể thức gửi tiết kiệm này.

Lời giải:

Số tiền lãi mẹ bạn Minh nhận được là:

321 600 000 - 300 000 000 = 21 600 000 (đồng).

Tỉ số giữa số tiền lãi và số tiền gốc là:

21  600  000300  000  000=21  600  000  :  3  000  000300  000  000   :  3  000  000=7,2100=7,2%

Vậy lãi suất ngân hàng theo thể thức gửi tiết kiệm này là 7,2%/năm.

Bài 10 trang 28 Toán lớp 7 Tập 1: Bác Lan mua ba món hàng ở một siêu thị: Món hàng thứ nhất giá 125 000 đồng và được giảm giá 30%; món hàng thứ hai giá 300 000 đồng và được giảm giá 15%; món hàng thứ ba được giảm 40%. Tổng số tiền bác Lan phải thanh toán là 692 500 đồng. Hỏi giá tiền món hàng thứ ba lúc chưa giảm giá là bao nhiêu?

Lời giải:

Do món hàng thứ nhất được giảm giá 30% nên món hàng thứ nhất bác Lan chỉ cần trả số tiền bằng 100% - 30% = 70% giá tiền ban đầu.

Số tiền bác Lan cần trả cho món hàng thứ nhất là:

70% . 125 000 = 70100.125000 = 87 500 (đồng).

Do món hàng thứ hai được giảm giá 15% nên món hàng thứ hai bác Lan chỉ cần trả số tiền bằng 100% - 15% = 85% giá tiền ban đầu.

Số tiền bác Lan cần trả cho món hàng thứ hai là:

85% . 300 000 = 85100.300000 = 255 000 (đồng).

Số tiền bác Lan cần trả cho món hàng thứ ba khi đã giảm giá là:

692 500 - 87 500 - 255 000 = 350 000 (đồng).

Giá tiền khi đã giảm giá của món hàng thứ ba bằng 100% - 40% = 60% giá tiền ban đầu nên giá tiền ban đầu của món hàng thứ ba khi chưa giảm giá là:

350 000 : 60% = 350 000 : 60100 = 350 000 . 53 ≈ 583 333 (đồng).

Vậy giá tiền của món hàng thứ ba khi chưa giảm giá là khoảng 583 333 đồng.

Bài 11 trang 28 Toán lớp 7 Tập 1: Nhân ngày 30/4, một cửa hàng thời trang giảm giá 20% cho tất cả các sản phẩm. Đặc biệt nếu khách hàng nào có thẻ khách hàng thân thiết của cửa hàng thì được giảm giá thêm 10% trên giá đã giảm.

a) Chị Thanh là khách hàng thân thiết của cửa hàng, chị đã đến cửa hàng mua một chiếc váy có giá niêm yết là 800 000 đồng. Hỏi chị Thanh phải trả bao nhiêu tiền cho chiếc váy đó?

b) Cô Minh cũng là một khách hàng thân thiết của cửa hàng, cô đã mua một chiếc túi xách và đã phải trả số tiền là 864 000 đồng. Hỏi giá ban đầu của chiếc túi xách đó là bao nhiêu?

Lời giải:

Giá tiền của sản phẩm khi không có thẻ khách hàng thân thiết bằng 100% - 20% = 80% giá tiền ban đầu.

Khi có thẻ khách hàng thân thiết thì giá của sản phẩm được giảm thêm 10% trên giá đã giảm nên giá tiền của sản phẩm khi có thẻ khách hàng thân thiết bằng 100% - 10% = 90% giá tiền đã giảm.

Giá tiền của sản phẩm khi được giảm giá nhân dịp 30/4 và có thẻ khách hàng thân thiết bằng 90% . 80% = 90100.80100=72100=72% giá tiền ban đầu.

a) Chị Thanh phải trả số tiền cho chiếc váy đó là:

72% . 800 000 = 72100. 800 000 = 576 000 (đồng).

Vậy chị Thanh cần trả 576 000 đồng cho chiếc váy.

b) Giá ban đầu của chiếc túi xách đó là:

864 000 : 72% = 864 000 : 72100 = 864 000 . 2518 = 1 200 000 (đồng).

Vậy giá tiền ban đầu của chiếc túi xách là 1 200 000 đồng.

Lý thuyết Toán 7 Bài tập cuối chương 1 - Chân trời sáng tạo

1. Số hữu tỉ

- Số hữu tỉ là số được viết dưới dạng phân số ab với a, b ∈ ℤ, b ¹ 0.

- Các phân số bằng nhau biểu diễn cùng một số hữu tỉ.

- Tập hợp các số hữu tỉ được kí hiệu là ℚ.

Ví dụ:

• Các số 45;−910;3−8 là các số hữu tỉ.

• Các số 5; −3,4; 325 là các số hữu tỉ vì:

5 = 51 = 102 = …;

−3,4 = −3410 = −175 = …;

325= 175 = 3410 = …

- Chú ý: Mỗi số nguyên là một số hữu tỉ.

2. Thứ tự trong tập hợp các số hữu tỉ

- Với hai số hữu tỉ bất kì x, y ta luôn có: hoặc x = y hoặc x < y hoặc x > y.

- Số hữu tỉ lớn hơn 0 gọi là số hữu tỉ dương.

Số hữu tỉ bé hơn 0 gọi là số hữu tỉ âm.

Số hữu tỉ 0 không là số hữu tỉ dương cũng không là số hữu tỉ âm.

Ví dụ: So sánh các cặp số hữu tỉ sau:

a) −0,8 và −15;

b) −823 và 0.

Hướng dẫn giải

a) −0,8 và −15

Ta có −0,8 = −810 và −15=−210.

Vì −8 < −2 và 10 > 0 nên −810<−210.

Vậy - 0,8 < −15.

b) −823 và 0

Ta có −823= −263 và 0 = 03.

Vì −26 < 0 và 3 > 0 nên −263<03.

Vậy −823 < 0.

Chú ý: Số hữu tỉ dương luôn luôn lớn hơn số hữu tỉ âm.

Ví dụ: Hãy sắp xếp các số hữu tỉ sau đây theo thứ tự tăng dần: 15,− 25,37,− 13,0.

Hướng dẫn giải

• Ta so sánh −25; −13và 0.

Có: −25  =  −615; −13 = −515 và 0=015.

Vì -6 < -5 < 0 nên −615<−515 < 015.

Do đó −25<−13<0. (1)

• Ta so sánh 15 với 37.

Có: 15 = 735 và 37 = 1535.

Vì 7 < 15 nên 735 < 1535.

Do đó 15<37. (2)

Lại có số hữu tỉ dương luôn lớn hơn số hữu tỉ âm. (3)

Từ (1), (2) và (3) ta có: −25<−13<0<  15  <37.

Vậy sắp xếp các số theo thứ tự tăng dần là: − 25; − 13; 0; 15; 37 .

3. Biểu diễn số hữu tỉ trên trục số

- Trên trục số, mỗi số hữu tỉ được biểu diễn bởi một điểm. Điểm biểu diễn số hữu tỉ x được gọi là điểm x.

- Với hai số hữu tỉ bất kì x, y, nếu x < y thì trên trục số nằm ngang, điểm x ở bên trái điểm y.

Ví dụ:

+ Để biểu diễn số hữu tỉ 54 ta làm như sau:

• Chia đoạn thẳng đơn vị thành bốn phần bằng nhau, ta được đoạn thẳng mới bằng 14 đơn vị cũ.

• Số hữu tỉ 54 được biểu diễn bởi điểm A nằm bên phải điểm 0 và cách điểm 0 một đoạn bằng 5 đơn vị mới như trong hình dưới.

+ Để biểu diễn số hữu tỉ 4−3 trên trục số ta làm như sau:

• Viết 2−3 dưới dạng phân số với mẫu số dương 2−3=−23.

• Chia đoạn thẳng đơn vị thành ba phần bằng nhau, ta được đoạn đơn vị mới bằng 13 đơn vị cũ.

• Số hữu tỉ 2−3 được biểu diễn bởi điểm B nằm bên trái điểm 0 và cách điểm 0 một đoạn bằng 2 đơn vị mới như hình dưới.

4. Số đối của một số hữu tỉ

- Hai số hữu tỉ có điểm biểu diễn trên trục số cách đều và nằm về hai phía điểm gốc O là hai số đối nhau, số này gọi là số đối của số kia.

- Số đối của số hữu tỉ x kí hiệu là −x.

Ví dụ:

−58 là số đối của 58;58 là số đối của −58

0,123 là số đối của −0,123; −0,123 là số đối của 0,123.

Số đối của 112 (có 112=32) là −32 và ta viết là −112 .

Chú ý:

- Mọi số hữu tỉ đều có một số đối.

- Số đối của số 0 là số 0.

- Với hai số hữu tỉ âm, số nào có số đối lớn hơn thì số đó nhỏ hơn.

Ví dụ: Tìm số đối của mỗi số sau: 1219;−16; -2,22; 0; 234.

Hướng dẫn giải

Số đối của số 1219 là số -1219

Số đối của số −16 là số 16

Số đối của số -2,22 là số 2,22.

Số đối của số 0 là số 0.

Số đối của số 234=114là số -114ta viết là −234.

5. Cộng, trừ hai số hữu tỉ

Để cộng, trừ hai số hữu tỉ x, y, ta có thể viết chúng dưới dạng hai phân số rồi áp dụng quy tắc cộng, trừ phân số.

Ví dụ: Tính:

a) 0,3 + 2−3 ;

b) 256 − (−4).

Hướng dẫn giải

a) 0,3 + 2−3 = 310 + −23

930+− 2030=9+−2030=−1130

b) 256 − (−4) = 176+41

176+246=17+246=416 .

6. Tính chất của phép cộng số hữu tỉ

Phép cộng số hữu tỉ cũng có các tính chất như phép cộng số nguyên: giao hoán, kết hợp và cộng với số 0.

Ví dụ: Tính một cách hợp lí:

−310+0,125+−710+0,875+45

Hướng dẫn giải

Ta có: −310+0,125+−710+0,875+45

= −310+−710+0,125+0,875+45 (tính chất giao hoán)

= (−310+−710)+(0,125+0,875)+45 (tính chất kết hợp)

= − 1 + 1 + 45

= 0 + 45 = 45 (cộng với số 0)

7. Nhân hai số hữu tỉ

Cho x, y là hai số hữu tỉ: x = ab , y = cd , ta có x . y = ab.cd = a.cb.d .

Ví dụ 1: Tính:

a) 238.−35;

b) 5,75 .910.

Hướng dẫn giải

a) 238.−35=198.−35

=19.−38.5=−5740

b) 5,75.910=575100.910

=575:25100:25.910=234.910

=23.94.10=20740

Ví dụ 2: Một mảnh vườn hình bình hành có đường cao bằng 24,8 m, độ dài đáy bằng 32 chiều cao. Tính diện tích mảnh vườn đó.

Hướng dẫn giải

Độ dài đáy mảnh vườn hình bình hành là:

32. 24,8 = 37,2 (m).

Diện tích mảnh vườn hình bình hành là:

37,2 . 24,8 = 922,56 (m2).

Vậy diện tích mảnh vườn hình bình hành là 922,56 m2.

8. Tính chất của phép nhân số hữu tỉ

Phép nhân số hữu tỉ cũng có các tính chất như phép nhân số nguyên: giao hoán, kết hợp, nhân với số 1, tính chất phân phối của phép nhân đối với phép cộng.

Ví dụ: Tính một cách hợp lí:

a) A = 9−8.415−89.3

b) B = −83.211−211.53.

Hướng dẫn giải

a) A = 9−8.415−89.3

= 9−8.−89.415. 3 (tính chất giao hoán)

=(9-8.−89).415. 3 (tính chất kết hợp)

= 1. 45 = 45 . (nhân với số 1)

b) B = −83.211−211.53.

= 211.(-83-53) . (phân phối của phép nhân đối với phép cộng)

= 211.-8-53 .

= 211.-133 .

= 2.(-13)11.3

= −2633.

9. Chia hai số hữu tỉ

Cho x, y là hai số hữu tỉ: x = ab , y = cd (y ≠ 0), ta có x : y = ab:cd=ab.dc=a.db.c

Ví dụ: Tính:

a) −125:(−6,5)

b) 512:−23.

Hướng dẫn giải

a) −125:(−6,5)=−125:-6510

=−125:−132=−125.2−13

= −12 . 25 . −13=2465.

b) 512  :  −23

=112:−23=112.3−2

= 11  . 32.−2=33−4=−334.

Chú ý:

Thương của phép chia số hữu tỉ x cho số hữu tỉ y (y ≠ 0) gọi là tỉ số của hai số x và y, kí hiệu là xy hay x : y.

10. Luỹ thừa với số mũ tự nhiên

- Luỹ thừa bậc n của một số hữu tỉ x, kí hiệu xn , là tích của n thừa số x.

xn = (x ∈ ℚ, n ∈ ℕ, n >1).

- Ta đọc xn là “x mũ n” hoặc “x luỹ thừa n” hoặc “luỹ thừa bậc n của x”.

- Số x được gọi là cơ số, n gọi là số mũ.

- Quy ước:

• x1 = x;

• x0 = 1 (x ≠ 0).

Ví dụ: Viết các luỹ thừa sau dưới dạng tích các số:

a) −342;

b) (0,8)4.

Hướng dẫn giải

a) −342 = −34.−34;

b) (0,8)4 = 0,8 . 0,8 . 0,8 . 0,8.

- Chú ý:

Khi viết số hữu tỉ x dưới dạng ab (a, b ∈ ℤ, b ≠ 0) ta có:

abn=ab.ab.  ...  .ab⏟n  thua  so=a . a.  ...  . ab . b .  ...  .b⏞n  thua  so⏟n  thua  so=anbn

Vậy abn=anbn.

Ví dụ: Tính:

a) 143 ;

b) (−0,125)2.

Hướng dẫn giải

a) 143=1343=164 ;

b) −0,1252=−182=(−1)282=164 .

11. Tích và thương của hai luỹ thừa cùng cơ số

- Khi nhân hai luỹ thừa cùng cơ số, ta giữ nguyên cơ số và cộng hai số mũ.

xm . xn = xm+n

- Khi chia hai luỹ thừa cùng cơ số khác 0, ta giữ nguyên cơ số và lấy số mũ của luỹ thừa bị chia trừ đi số mũ của luỹ thừa chia.

xm : xn = xm - n (x ¹ 0, m ³ n)

Ví dụ: Viết các biểu thức sau dưới dạng luỹ thừa của một số hữu tỉ:

a) (−4,1)5 : (−4,1)3;

b) 353.354.

Hướng dẫn giải

a) (−4,1)5 : (−4,1)3 = (−4,1)5 - 3 = (−4,1)2 ;

b) 353.354=353+4=357 .

12. Luỹ thừa của luỹ thừa

- Khi tính luỹ thừa của một luỹ thừa, ta giữ nguyên cơ số và nhân hai số mũ.

(xm )n = xm.n

Ví dụ: Viết các biểu thức sau dưới dạng luỹ thừa của một số hữu tỉ:

a) −1523;

b) 0,924.

Hướng dẫn giải

a) −1523=−152 . 3=−156 ;

b) 0,924=0,92 . 4=0,98 .

13. Quy tắc dấu ngoặc

- Khi bỏ dấu ngoặc, nếu đằng trước dấu ngoặc:

• Có dấu “+”, thì vẫn giữ nguyên dấu của các số hạng trong ngoặc.

x + (y + z - t) = x + y + z - t

• Có dấu “−”, thì phải đổi dấu tất cả các số hạng trong ngoặc.

x - (y + z - t) = x - y - z + t

Ví dụ: Tính

a) 314+0,4−14 ;

b) 0,5+113−43+14.

Hướng dẫn giải

a) 314+0,4−14

= 134+410−14

= 134+25−14

= 134+25−14

= 134−14+25

= =124+25=3+25

= 155+25=175 .

b) 0,5+113−43+14.

= 12+43−43+14

= 12+43−43−14

= 12−14

= 24−14=14 .

14. Quy tắc chuyển vế

Khi chuyển một số hạng từ vế này sang vế kia của một đẳng thức, ta phải đổi dấu số hạng đó.

Với mọi x, y, z ∈ ℚ: Nếu x + y = z thì x = z - y.

Ví dụ: Tìm x, biết:

a) x+3,5=312 ;

b) −34+x=56 .

Hướng dẫn giải

a) x+3,5=312

x=312−3,5

x=312−72

x=242

x=12

Vậy x=12 .

b) −34+x=56

x=56−−34

x=1012+912

x=1912

Vậy .

15. Thứ tự thực hiện các phép tính

- Thứ tự thực hiện các phép tính trong một biểu thức đối với biểu thức không có dấu ngoặc:

• Nếu biểu thức chỉ có phép cộng, trừ hoặc chỉ có phép nhân, chia, ta thực hiện phép tính theo thứ tự từ trái sang phải.

• Nếu biểu thức có các phép cộng, trừ, nhân, chia, nâng lên luỹ thừa, ta thực hiện:

Luỹ thừa → Nhân và chia → Cộng và trừ

- Thứ tự thực hiện các phép tính đối với biểu thức có dấu ngoặc:

() → [] → {}

Ví dụ: Tính:

a) 13+74−56:−0,5 ;

b) −315−−115:152:310 .

Hướng dẫn giải

a) 13+74−56:−0,5

= 13+74−56:−12

= 13+74−56.−21

= 13+74−5.−26.1

= 13+74−−53

= 13+74+53

= 13+53+74

= 63+74=2+74

= 84+74=154.

b) −315−−115:152:310

= − 165−− 115:1252.103

= − 165−− 115:125.103

= − 165−− 115.251.103

= − 165−−2515.103

= − 165+2515.103

= − 4815+2515.103

= −2315.103=−469 .

Xem thêm lời giải bài tập Toán lớp 7 Chân trời sáng tạo hay, chi tiết khác:

Bài 1: Tập hợp các số hữu tỉ

Bài 2: Các phép tính với số hữu tỉ

Bài 3: Lũy thừa của một số hữu tỉ

Bài 4: Quy tắc dấu ngoặc và quy tắc chuyển vế

Bài 5: Hoạt động thực hành và trải nghiệm: Thực hành tính tiền điện

Xem thêm tài liệu Toán lớp 7 Chân trời sáng tạo hay, chi tiết khác:

Lý thuyết Bài tập cuối chương 1

Trắc nghiệm Ôn tập chương 1